Hipoteza Goldbacha

Na początek kilka słów o samej hipotezie, później rozłożymy ją na części pierwsze.

Jest to jeden z czterech podpunktów ósmego problemu Hilberta, hipoteza Bernharda Riemanna jest również częścią tego problemu (problem milenijny).

Oryginalnie hipoteza Goldbacha brzmiała: "każdą liczbę parzystą począwszy od 6 da się zapisać za pomocą

sumy trzech liczb pierwszych", lecz Leonhard Euler poprawił go, twierdząc, że "każdą liczbę

parzystą począwszy od 4 da się zapisać za pomocą sumy dwóch liczb pierwszych" i tak już zostało.

Hipoteza została przyjęta z poprawką Eulera, ale nazwa została oryginalna.

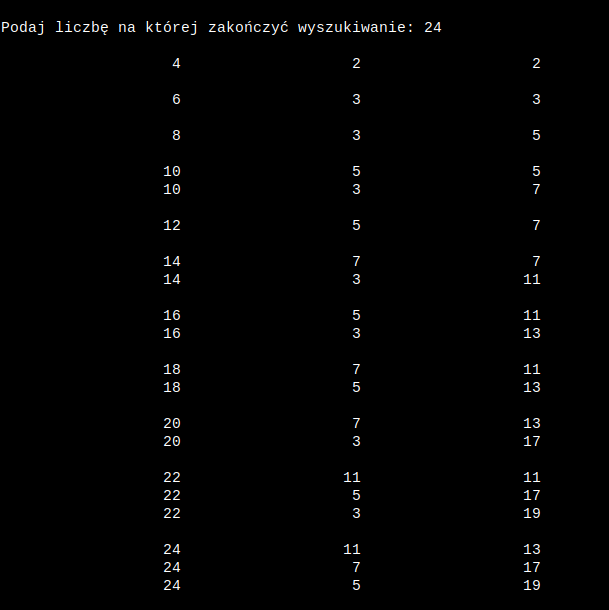
Oto prosty przykład z samego początku osi liczbowej (zakres 4 - 24).

Już na samym początku można zauważyć, że ilość par zwiększa się im większa liczba.

Ale jak to bywa z liczbami pierwszymi jest nieregularnie (różnice ilości par między sąsiednimi liczbami są czasem wręcz abstrakcyjne).

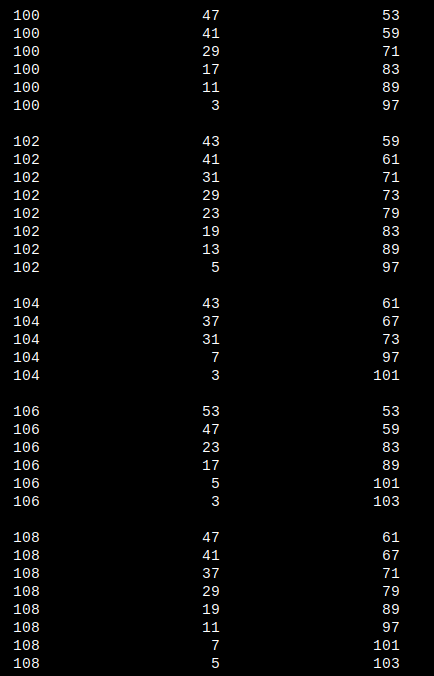
Oto zakres odnalezionych par w zakresie 100 - 108

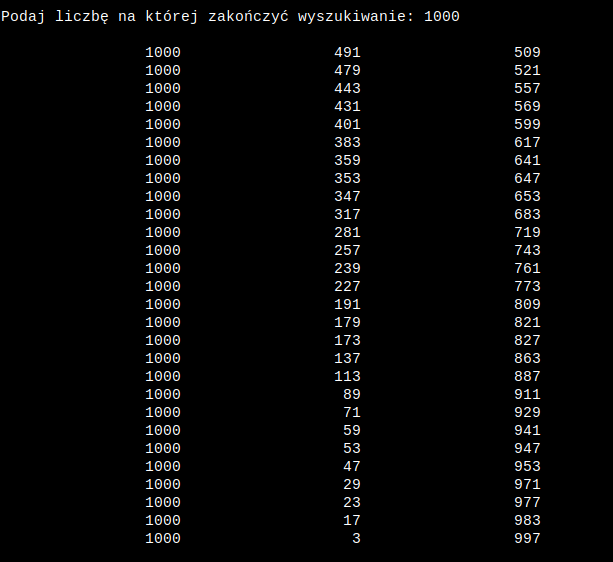
Jeszcze pokażę rozkład tysiąca i kilka wykresów - następnie przejdę do strony technicznej.

Jedna rzecz mnie jeszcze bardzo zaciekawiła, bo problem tkwi w tym,

czy hipoteza sprawdzi się do nieskończoności, ja obstawiam, że tak już od dawna,

ale ostatnio wziąłem sporą ilość liczb, program szukał tylko jednej pary najbliżej połowy sprawdzanej liczby,

skakał do następnej parzystej itd. (powyżej jest treść hipotezy, także jedna para już ją potwierdza).

Utworzyłem plik z danymi na 291MB i załadowałem dane do wykresu. Oto wynik:

Tu jest wykres z mapką występowania liczb pierwszych w parach do 1000:

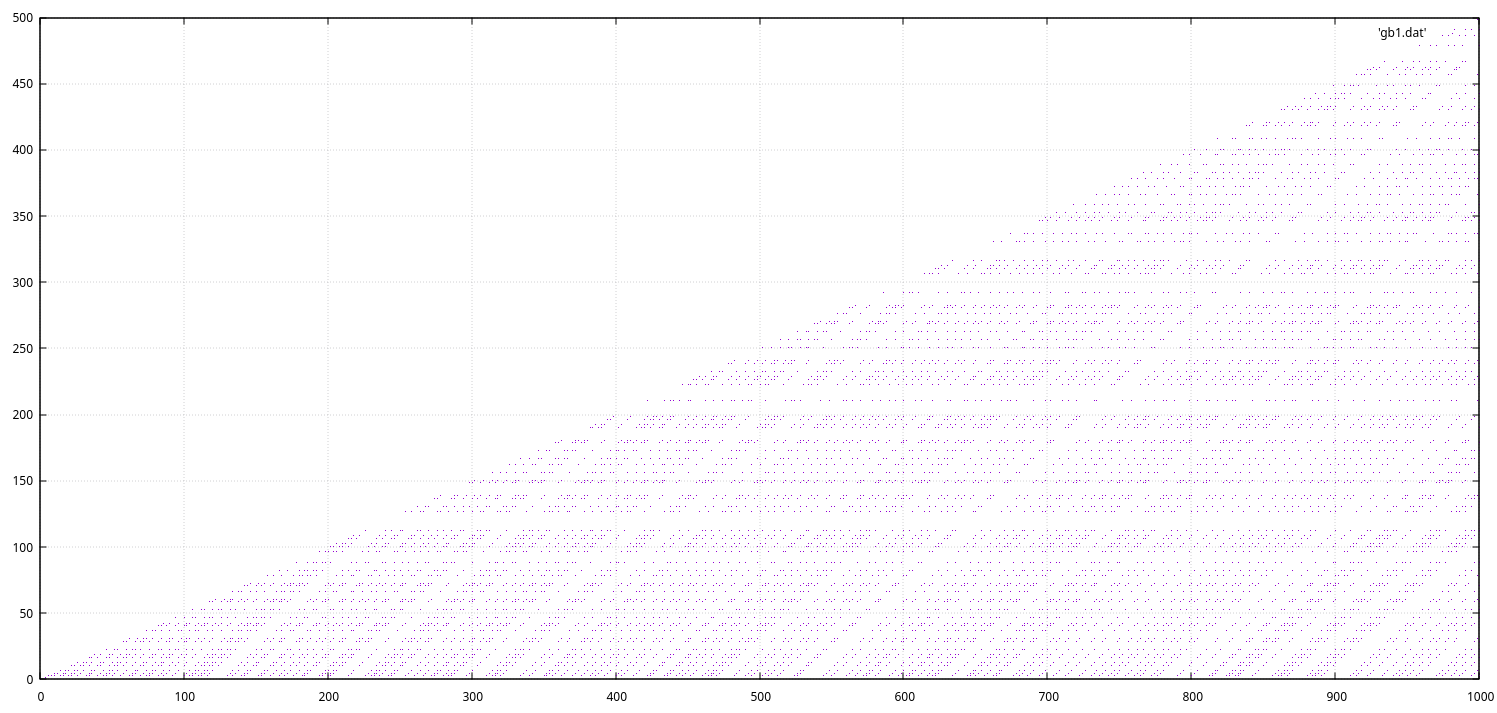
...a tu dla 10000:

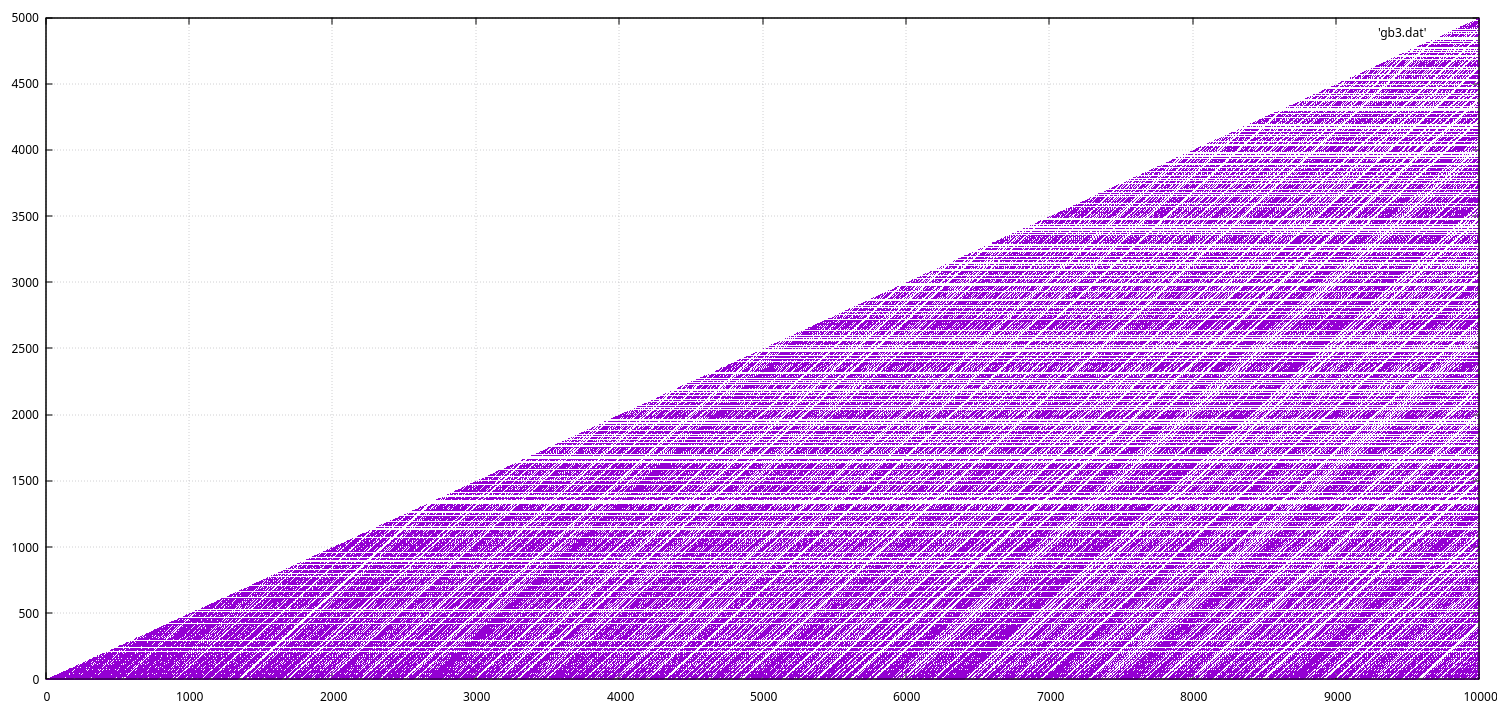
Dość interesujące...