Złota proporcja w złotych ciągach - (nie tylko ciąg Fibonacciego to potrafi)

Złote ciągi tworzy się poprzez dodanie dwóch sąsiednich cyfr, co daje następną - tu wzór na ciąg Fibonacciego [fib = (fib - 1) + (fib - 2)]
Każdy inny złoty ciąg oblicza się tak samo, wszystko zależy od pierwszych dwóch liczb.
Ciągiem, który nas otacza na każdym kroku jest ciąg Fibonacciego.
Nie będę się tu nad tym rozwodził, odsyłam do Youtube'a, jest tam dość fajny materiał na ten temat.
Jak koniecznie chcesz sprawdzić, czy masz go gdzieś w pobliżu weź kwiat,
przelicz płatki i sprawdź, czy zgadza się z którymś wyrazem ciągu.

Kod źródłowy obliczający ciąg Fibonacciego, ciąg Lucas'a i jeden ciąg jest przy każdym uruchomieniu
losowany, chciałem tym sposobem pokazać, że złotą liczbę można uzyskać nie tylko z tych dwóch ciągów,
ale także z każdego innego, którego kolejne wyrazy powstają w ten sam sposób co ciąg Fibonacciego i Lucas'a.
Jakby ktoś nie wiedział, to złotą liczbę uzyskuje się przez podzielenie dwóch
sąsiednich wyrazów (większego przez mniejszy), im dalsze wyrazy zostaną podzielone, tym większe będzie przybliżenie.
Wszystkie obliczenia tak zostały ustawione, aby zakańczać się po uzyskaniu max. przybliżenia dla zmiennej double -
- (liczba zmiennopozycyjna, podwójnej precyzji).

Na końcu jest jeszcze obliczona złota liczba za pomocą wzoru i mała ciekawostka, która stanowi dla mnie zagadkę, której jeszcze nie rozwiązałem.

Kod źródłowy w ANSI C:

#include <stdio.h>
#include <stdlib.h>
#include <time.h>
#include <math.h>

int main(void) {
     long fib[90], luc[90], ran[90];
     short sign;

     printf("\n---------- TWO MOST POPULAR AND ONE RANDOM GOLDEN SERIES & PHI TRICK ----------\n");

     fib[0] = 1;
     fib[1] = 1;

     luc[0] = 2;
     luc[1] = 1;

     srand(time(NULL));
     sign = rand() % 10;

     ran[0] = rand() % 1000;
     ran[1] = rand() % 1000;

     if(sign < 5)
          ran[1] *= -1;

     for(int i = 2; i < 90; i++) {
          fib[i] = fib[i - 2] + fib[i - 1];
          luc[i] = luc[i - 2] + luc[i - 1];
          if(i <= 51)
               ran[i] = ran[i - 2] + ran[i - 1];
          else(ran[i] = 0);
     }

     printf("\n      Fibonacci Sequence                              Lucas Sequence                              Random Sequence\n");

     for(int i = 0; i < 90; i++) {
          if(i <= 51)
               printf("\n%3d. %20ld %20ld %20ld", i + 1, fib[i], luc[i], ran[i]);
          else printf(" %3d. %20ld %20ld", i + 1, fib[i], luc[i]);
          if(i == 53) printf("\t\t Enough numbers to reach maximum approximation");
     }

     printf("\n\n---------- PHI CALCULATED FROM FIBONACCI SERIES NUMBERS ----------\n");

     for(int i = 0; i < 40; i++) {
          printf("\nPHI = %.48lf -----> %ld / %ld --> fib(%d) / fib(%d)", (double)fib[i + 1] / (double)fib[i], fib[i + 1], fib[i], i + 2, i + 1);
     }

     printf("\n\n---------- PHI CALCULATED FROM LUCAS SERIES NUMBERS ----------\n");

     for(int i = 0; i < 40; i++) {
          printf("\nPHI = %.48lf -----> %ld / %ld --> luc(%d) / luc(%d)", (double)luc[i + 1] / (double)luc[i], luc[i + 1], luc[i], i + 2, i + 1);
     }

     printf("\n\n---------- PHI CALCULATED FROM RANDOM SERIES NUMBERS ----------\n");

     for(int i = 0; i < 51; i++) {
          if(ran[i] != 0)
               printf("\nPHI = %.48lf -----> %ld / %ld --> seq(%d) / seq(%d)", (double)ran[i + 1] / (double)ran[i], ran[i + 1], ran[i], i + 2, i + 1);
          else printf("\n\t\t\t\tseq(%d) / seq(%d) ---------> DIVISION BY 0 !!!", i + 2, i + 1);
     }

     printf("\n\n---------- PHI CALCULATED BY FORMULA ----------\n");

     printf("\nPHI = %.48lf -----> ((sqrt(5) + 1) / 2)", ((sqrt(5) + 1) / 2));

     printf("\n\n");

     return 0;
}

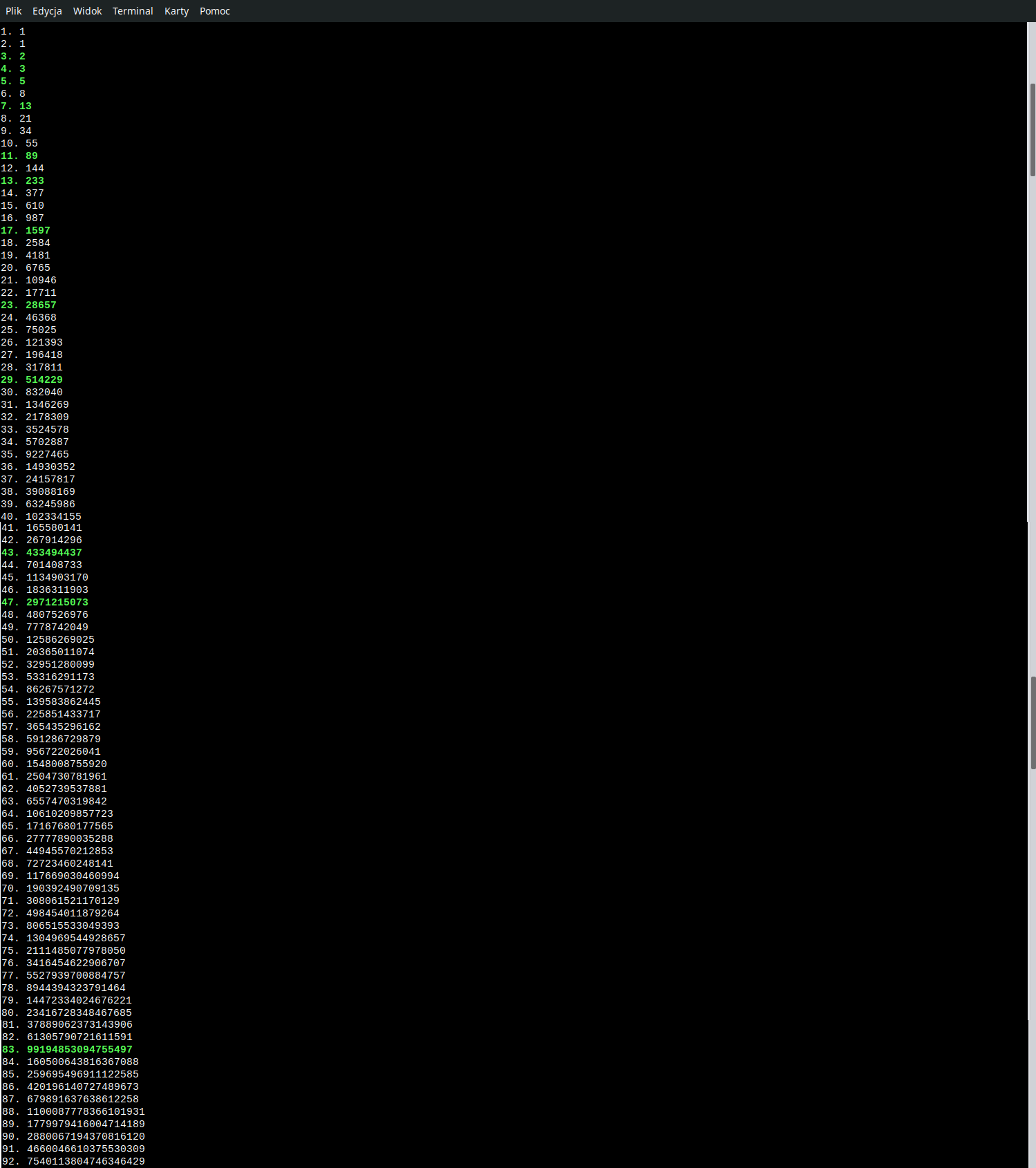
Poniżej zrzut ekranu z obliczeń powyższego kodu:

Znalazłem jeszcze coś dziwnego:

Każda liczba ciągu Fibonacciego, która jest liczbą pierwszą z wyjątkiem czwartej liczby - czyli 3,
ma liczbę porządkową, która jest również liczbą pierwszą, może to przypadek, bo test jest zrobiony
tylko dla 92 liczb ciągu (max. 64 bitowe).
Testowane sitem Eratosthenesa, także nie ma mowy o pomyłce.